Thesis
 My Ph.D. thesis is titled An Integrated Framework for Modeling and Predicting Spatiotemporal Phenomena in Urban Environments, which is the cumulative work of my four and a half years’ journey. In a nutshell, it is about solving urban problems using spatiotemporal data and machine learning. The particular urban problems it addresses are: human mobility prediction, traffic speed prediction, and crime prediction. In the thesis, I propose a generic solution framework for urban problems using spatiotemporal data and machine learning. The dissertation committee consists of Professors Hoong Chuin Lau, Robert J. Kauffman, Akshat Kumar, and Siyuan Liu.
My Ph.D. thesis is titled An Integrated Framework for Modeling and Predicting Spatiotemporal Phenomena in Urban Environments, which is the cumulative work of my four and a half years’ journey. In a nutshell, it is about solving urban problems using spatiotemporal data and machine learning. The particular urban problems it addresses are: human mobility prediction, traffic speed prediction, and crime prediction. In the thesis, I propose a generic solution framework for urban problems using spatiotemporal data and machine learning. The dissertation committee consists of Professors Hoong Chuin Lau, Robert J. Kauffman, Akshat Kumar, and Siyuan Liu.
- On September 21, 2017, I have successfully defended my thesis. [Get PDF] [Slides]
- On March 25, 2018, I gave a stripped-down presentation of the thesis at FOSSASIA 2018. [Slides]
The following publications form the core parts of my thesis:
-
Jonathan Chase, Jiali Du, Na Fu, Truc Viet Le and Hoong Chuin Lau. Law Enforcement Resource Optimization with Response Time Guarantees. IEEE SSCI 2017. [Read more]
-
Truc Viet Le, Richard J. Oentaryo, Siyuan Liu and Hoong Chuin Lau. Local Gaussian Processes for Efficient Fine-Grained Traffic Speed Prediction. IEEE Transactions on Big Data (2016). [Read more]
-
Truc Viet Le, Siyuan Liu and Hoong Chuin Lau. A Reinforcement Learning Framework for Trajectory Prediction Under Uncertainty and Budget Constraint. ECAI 2016. [Get PDF] [Slides]
-
Truc Viet Le, Siyuan Liu, Hoong Chuin Lau and Ramayya Krishnan. Predicting Bundles of Spatial Locations from Learning Revealed Preference Data. AAMAS 2015. [Get PDF] [Slides]
Abstract (click to expand)
This thesis proposes a general solution framework that integrates methods in machine learning in creative ways to solve a diverse set of problems arising in urban environments. It particularly focuses on modeling spatiotemporal data for the purpose of predicting urban phenomena. Concretely, the framework is applied to solve three specific real-world problems: human mobility prediction, traffic speed prediction and incident prediction.
For human mobility prediction, I use visitor trajectories collected a large theme park in Singapore as a simplified microcosm of an urban area. A trajectory is an ordered sequence of attraction visits and corresponding timestamps produced by a visitor. This problem has two related subproblems: (spatial) bundle prediction and trajectory prediction. In the first problem, I apply the framework to predict a bundle (i.e., an unordered set) of attractions that a given visitor would visit given a time budget. In the second problem, the framework is applied to predict the visitor's actual trajectory given the current partial trajectory and time budget. In both problems, I apply the methods of trajectory clustering, hidden Markov model, revealed preference learning and (inverse) reinforcement learning in the integrated framework.
In traffic speed prediction, I wish to predict the spatiotemporal distribution of traffic speed over urban road networks. To this end, I propose local Gaussian processes which combine non-negative matrix (NMF) factorization with Gaussian process (GP) in order to enhance the efficiency of model training such that the solution could be deployed in real-time use cases. NMF is essentially a spatiotemporal clustering technique. The solution is extensively evaluated using real-world traffic data collected in two U.S. cities.
The incident prediction problem is about predicting the distribution of the number of crime incidents over urban areas in future time periods. Because of its similarity to the traffic prediction problem above, its solution greatly benefits from the GP model developed earlier. Particularly, the GP kernel function is inherited and extended to model the distribution of incidents in urban areas and their features. The proposed solution is evaluated using real-world incident data collected in a large Asian city.
Conceptually, this thesis uses big data and machine learning techniques to solve three separate urban problems, whose contribution belongs to the large category of urban computing. At the core, its technical contribution lies in the unification of separate solutions tailored to those problems into an integrated framework that reasons with spatiotemporal data and, thus, is highly generalizable to other problems of similar nature.
Overview
The figure below summarizes the machine learning models, spatiotemporal data and problems in urban environments studied in the thesis. In essence, it is a combination of machine learning models and spatiotemporal data that solves a diverse set of problems in urban environments. Synthesized from those methods and data, a common solution framework can be integrated that “abstracts away” the peculiar features of each of the individual problems.
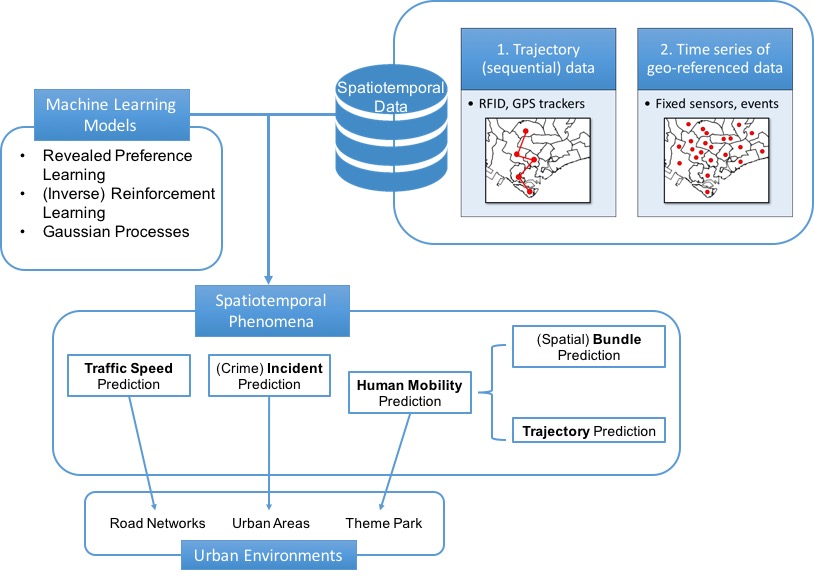
I call this an integrated framework because it provides a high-level abstraction of the problem-solving process that can be generalized and extended to solve other urban problems of similar nature. As illustrated in the above figure, even though the data and their problems are intrinsically tied together, the separation of data from problems gives rise to the synthesis and abstraction of processes that make up the proposed integrated framework.
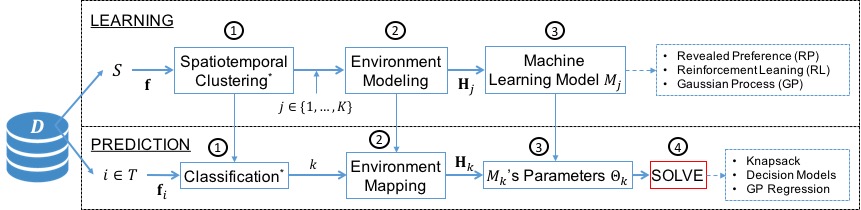
Thus, the main contribution of the thesis is to extend the Urban Data Analytics component of the General Framework of Urban Computing proposed by Zheng et al. (2014). The integrated framework is illustrated in the figure below. Refer to Chapter 3 of the thesis for detailed description.
Urban Problems
The particular urban problems that the thesis solves are:
- Human mobility predictionn [Chapters 4 and 5]
- Real-time traffic speed prediction [Chapter 6]
- Crime distribution prediction [Chapter 7]
 Home
Home